凸优化问题¶
1. 简介¶
凸优化问题具有这样的形式:
其中,目标函数和约束函数 \(f_0, \dots, f_m\) 是凸函数。
一个函数 \(f: \mathbb{R}^n \to \mathbb{R}\) 是凸函数,当且仅当对于任意的 \(x, y \in \mathbb{R}^n\) 和 \(\theta \in [0, 1]\),满足以下不等式:
直观的几何理解是,凸函数上任意两点间的连线总在函数图像的上方或者重合。
教科书认为,若一个优化问题可以被化作凸优化问题,那么这个问题基本可以说是解决了,就是这样强大。比如一些经典的问题,如最小二乘问题和线性规划问题,实际上也是凸优化问题,他们已经有了完整的解决方案。历史上,苏联的科学家 Nesterov 与 Nemirovski 最早发现,使得优化问题变“容易”的关键性质,是函数的凸性,并且,他们引入了内点法来有效求解凸问题。实际中很少能像最小二乘或者函数求导那样简单地能获得问题的解析解(代数表达式),但是只要能化为凸优化问题,往往就意味着可以利用高效的数值方法求出问题的最优解。
2. 对偶¶
学过微积分的读者,应该对这样的问题有印象:求解含有等式约束的多变量极值问题。当时我们的做法是引入拉格朗日函数,将等式约束问题转化为无条件约束问题。其几何意义就是获得几个曲面的的交线,在这个交线上寻找最优点。
在优化理论中,也有类似的概念,称为对偶(duality)。它将一个有约束问题转化成一个无约束问题,后者称为对偶问题。
我们考虑这样的优化问题:
那么其拉格朗日函数表示为:
其中:
- \(\lambda_i \geq 0\) 是不等式约束的拉格朗日乘子;
- \(\nu_j\) 是等式约束的拉格朗日乘子
定义拉格朗日对偶函数是拉格朗日函数的关于变量 \(x\) 取得的最小值:
我们容易证明这样的性质:对偶函数构成原问题最优值 \(p^*\) 的下界,即对任意 \(\lambda>0, \nu\) 都有:
这意味着我们只要求出 \(g(\lambda, \nu)\) 的上界 \(d^*\),就可以逼近原问题的下界 \(p^*\)。
于是,我们就这样定义原问题的对偶问题:
很容易知道,即使原问题不是凸的,对偶问题也是凸优化问题。
我们容易得到: \(d^* \leq p^*\)。根据是否取到等号来判断是强对偶性或者是弱对偶性。所以我们有时可以通过求对偶问题的解,再转化成原问题的解。
原问题与对偶问题的关系大致如下所示(图是网上别人画的):
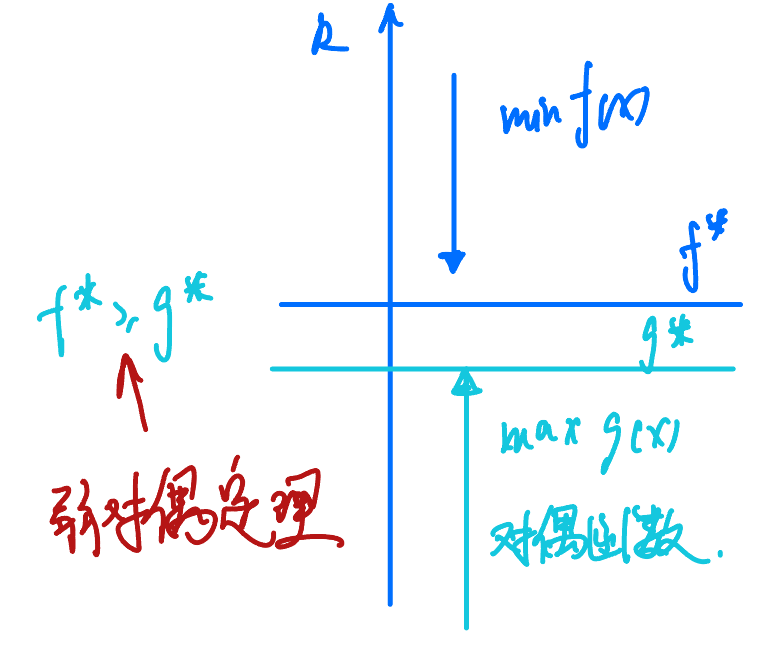
对于一个满足强对偶性的问题,若这个问题的最优解为 \(x^*\),其对偶问题的解是 \((\lambda^*, \nu^*)\)。则它们满足 KKT(Karush-Kuhn-Tucker) 条件:
- 原始可行性:
- 对偶可行性:
- 互补松弛条件:
- 拉格朗日梯度条件:
KKT 条件是一组最优解的必要条件。若原问题也是凸的,则 KKT 条件成为解的充分条件。
KKT 条件非常重要,对一些问题来说,可以将求解原问题转化成求解满足 KKT 条件的点,从而找到最优解。
下面,我们介绍一些典型的凸优化问题及其算法。目前典型的凸优化问题都有比较成熟的软件支持了。
3. 无约束优化问题,梯度下降法¶
假设我们构造出了一个无约束优化问题:
我们想找到其最优解,经典的方法是梯度下降法。原理是在一个初始点 \(x_k\) 进行一阶泰勒展开:
于是不断地向负梯度方向进行迭代:
\(\lambda\) 是步长,可以是超参数,或者用搜索步长法确定。
直到收敛条件为止。
求解梯度的方法,简单的函数用解析法,复杂的函数可以用反向传播法进行自动微分计算。
实例:二次函数拟合¶
我们下面再用二次函数的拟合,来介绍一下优化方法。
假设我获得了 200 个点,其函数值是二次函数和高斯噪声的混合,我怎么对二次函数进行拟合呢?拟合问题是一个线性模型:
其中 A 是数据矩阵 \([x^2, x, 1]\) 向下叠 n 行,x 是我们要拟合的参数 \([a ,b ,c]^T\),\(y^*\) 是预测值矩阵。
我们希望求出最好的 x,使得 \(y^*\) 与实际的 \(y\) 相差最小,就可以得到这样无约束优化问题(用均方误差 MSE 作为损失函数):
其在点 x 处的梯度是:
当然我们前面已经求过了解析解:\(x = (A^TA)^{-1}A^Ty\)。但是当 \(A\) 巨大的时候,求逆会非常困难,不太可行,现代求逆的复杂度是 \(o(n^3)\)。
所以我们用梯度下降法进行求解。代码大致如下:
def gradient_descent(X, y, learning_rate=0.0001, epochs=1000):
theta = np.random.randn(3) # 随机初始化参数
m = len(y)
losses = []
for epoch in range(epochs):
gradients = 2/m * X.T @ (X @ theta - y)
theta = theta - learning_rate * gradients
loss = np.mean((X @ theta - y)**2)
losses.append(loss)
if epoch % 100 == 0:
print(f"Epoch {epoch}, Loss: {loss:.4f}")
return theta, losses
在深度学习中,上面的数据矩阵 X 会非常大,导致 gradient 和 loss 的计算都很困难。于是人们想到抽样的方法,每次只使用几个样本进行梯度的更新,而不是全部数据,这种方法就是所谓的小批量梯度下降(mini-batch GD)。
代码大致如下:
def mini_batch_gradient_descent(X, y, batch_size=32, learning_rate=0.0001, epochs=1000):
theta = np.random.randn(3)
m = len(y)
losses = []
for epoch in range(epochs):
shuffled_indices = np.random.permutation(m)
X_shuffled = X[shuffled_indices]
y_shuffled = y[shuffled_indices]
for i in range(0, m, batch_size):
X_batch = X_shuffled[i:i+batch_size]
y_batch = y_shuffled[i:i+batch_size]
batch_m = len(y_batch)
gradients = 2/batch_m * X_batch.T @ (X_batch @ theta - y_batch)
theta = theta - learning_rate * gradients
loss = np.mean((X @ theta - y)**2)
losses.append(loss)
if epoch % 100 == 0:
print(f"Epoch {epoch}, Loss: {loss:.4f}")
return theta, losses
一开始每进行一次梯度下降就是一个 epoch。后来都是小批量算法,有 batch 的概念。将数据随机打乱抽样成一个个 batch。每次这些 batch 遍历完所有数据为一个 epoch。
实际上深度学习问题,和上面二次函数的拟合问题,本质几乎一模一样。改变的只有模型、损失函数的计算、更新参数的方法。
在深度学习中,我们要求解一个最优模型,参数数量远大于上面的二次函数系数,因此梯度非常难以用解析的方式表达。但是没关系,反向传播算法解决了这个问题,每次我们计算出 loss,就可以用反向传播,计算出每一层的梯度,从而继续用梯度下降法来更新参数。
4. 约束优化问题,内点法¶
不等式约束的极小化问题,有一个非常好的方法,内点法。我们详细介绍一下。考虑问题的形式如下:
m 是约束条件个数,后面会用到。
简单起见,不考虑等式约束。如果有等式约束,最简单的方法就是使用代入法进行消元,转化成上述形式,再做。其他方法读书去了。
那么有不等式约束,应该怎么做呢?我们当然是想办法消除不等式约束。经典的方法是引入障碍函数(或者叫罚函数)。我们把问题重新表述成:
这个函数不可微,所以想办法用其他函数近似。比如说,用对数障碍函数。
其梯度为:
那么问题转化成:
其中 \(t>0\) 是确定近似精度的参数。\(t\) 越大,对数函数越平滑,越符合示性函数。
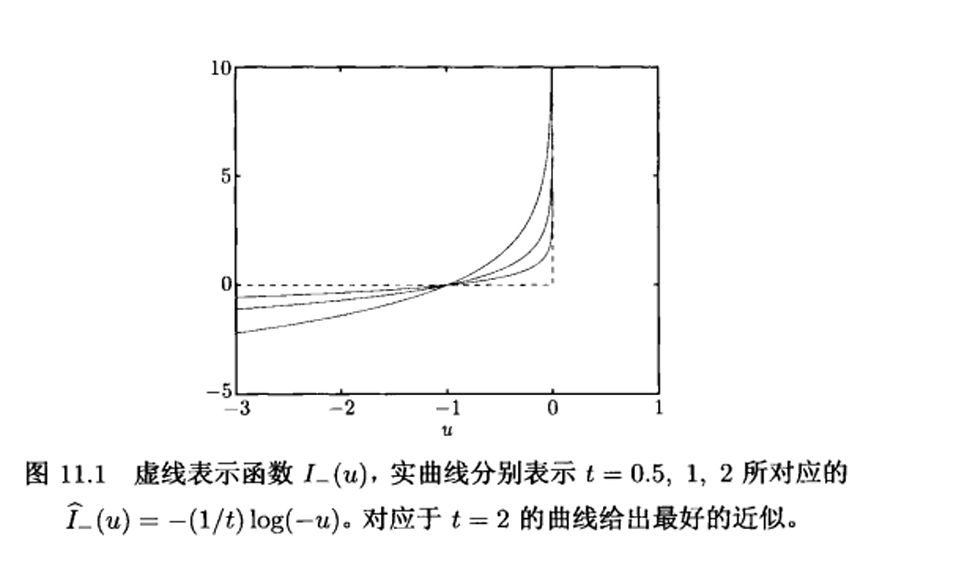
好,现在这问题变成了一个无约束优化问题。我们求解这个问题的最优解,就可以求得原问题的解的一个近似。这近似好吗?一开始我有所怀疑,但是接下来可以用数学,来说明是好的,因为可以看到我们可以通过增加 t 来改进近似精度。
为方便,下面我们考虑等价问题(1):
对任意一个 \(t\),我们将问题(1)的最优解记作 \(x^*(t)\)。可知,这些点 \(x^*(t)\) 都是在原问题的严格可行域内的,所以被叫做中心点(内点),这些点的集合叫做中心路径。
由 KKT 最优性条件,考虑(1)的拉格朗日梯度条件有:
回到原问题的拉格朗日函数:
如果令
则 \(x^*(t)\) 正好使拉格朗日函数达到最小,对应的对偶函数 \(g(\lambda)=\min_xL(x,\lambda)\)。(无需考虑 \(\lambda\) 是否独立)
于是,由弱对偶定理,有:
即:
这个不等式说明了,我们用近似方法求得的近似解 \(x^*(t)\) 是次最优解,并且随着 \(t\) 的增大,能逐渐收敛于最优解。
所以我们就可以想到这样的算法:从次优点向最优点逐步逼近,并增大 t,称为序列障碍法或路径跟踪法(SUMT)。算法伪代码如下
找一个严格可行的 x_0(不能在边界上,一定要是内点),确定初始 t_0>0,mu>1,eps>0
重复进行
1. 中心点步骤,以 x 为初始点,求解极小化问题 tf_0(x)+phi(x) 的解 x(t)
2. 更新 x = x(t)
3. 判断收敛误差是否 m/t <= mu,是则停止算法
4. 更新 t=mu*t。
上面的每次迭代找到新的中心点称为外迭代。找到中心点或是使用梯度下降,或是使用牛顿法,要做若干次迭代称为内迭代。由于中心点在可行集内部、中心路径朝着最优点走、使用了障碍函数,故被称为内点法/序列障碍法/中心路径法。
实例:线性规划¶
下面以线性规划问题为例来实现一个内点法。
考虑标准约束的线性规划问题:
其对数障碍函数为:
梯度为:
我们用内点法来实现,写出代码如下:
def interior_point(A, b, c, x0, t0=1, mu=20, epsilon=1e-8, max_iter=1000):
"""
内点法
参数:
A, b, c: 线性规划问题的参数,约束 A@x<=b, 求解 min c@x
x0: 初始点(必须严格可行)
t0: 初始障碍参数
mu: 障碍参数增长因子
epsilon: 收敛阈值
max_iter: 最大迭代次数
"""
m = len(b) # 不等式约束个数
t = t0
x = x0
for k in range(max_iter):
# solve min t*c@x+phi(x), get new_x
# phi(x) = -sum(ln(bi-ai*x))
new_x, loss = central_path(A, b, c, t, x)
x = new_x
if m / t <= epsilon:
return x, c @ x
t *= mu
loss = c @ x
return x, loss
中间求解中心路径的算法,我使用了梯度下降法。虽然教材使用牛顿法。注意,外部迭代是一定会在可行域内的,但是内部迭代不会,有可能会超出可行域,需要进行一步判断。
def gradient_descent(A, b, c, t, x0, lr=0.001, epoch=1000, eps=1e-8):
"""
用梯度下降法求解中心路径问题,求最优 x
"""
x = x0
loss = 0
last_loss = 0
last_x = 0
for i in range(epoch):
Ax = A @ x
bAx = b-Ax
# numpy 广播沿着纵向
grad_phi = np.sum(A.T / (bAx+eps), axis=1)
grad = grad_phi+t*c
last_x=x
x = x-lr*grad
last_loss = loss
# 判断是否是可行点,用梯度下降得到的结果,未必是可行点。
# 最优解一定是可行点没问题,但是梯度下降会震荡等等产生的结果未必是可行点,注意了。
# 所以这里加一个判断
if (np.all(b-A@x>0))==False:
x=last_x
lr=lr*0.5
continue
phi = -np.sum(np.log(b-A@x))
loss = t*c@x + phi
if np.abs(last_loss-loss) < eps or np.sum(np.abs(last_x-x)) < eps:
break
return x,loss
def central_path(A,b,c,t,x0):
"""
求解中心路径(内迭代),线性规划的中心路径最优化问题是:
min t*c@x+phi(x)
phi(x) = -sum(ln(bi-ai*x))
以 x0 为迭代初始点,求 x
"""
lr = 0.001
epoch = 200
x, loss = gradient_descent(A, b, c, t, x0, lr, epoch)
# x, loss = newton_method(A, b, c, t, x0, lr, epoch)
return x, loss
将官方代码和手写方法进行比较,可以看到几乎一致,内点法效果很好。
from scipy.optimize import linprog
import numpy as np
# 定义问题数据
c = np.array([-3, -5]) # 目标函数系数(取负值)
A = np.array([[1, 2], [2, 1], [-1, 0], [0, -1]]) # 不等式约束矩阵
b = np.array([10, 8, 0 ,0 ]) # 约束右侧值
# 官方求解
result = linprog(c, A_ub=A, b_ub=b, method='highs')
print("\n=== scipy.optimize.linprog 结果 ===")
print("最优解:", result.x)
print("最大利润:", -result.fun) # 目标值取负恢复最大值
print("状态:", result.message)
# 手写方法
x0 = np.array([1,1])
assert np.all(A @ x0 < b - 1e-6), "初始点不是严格可行的"
x, loss = interior_point(A, b, c, x0)
print("\n=== my result ===")
print("最优解:", x)
print("最大利润:", -loss) # 目标值取负恢复最大值
=== scipy.optimize.linprog 结果 ===
最优解: [2. 4.]
最大利润: 26.0
状态: Optimization terminated successfully. (HiGHS Status 7: Optimal)
=== my result ===
最优解: [1.98894776 4.00552612]
最大利润: 25.994473878868448
如果 t 和 初始 x_0 取的好,迭代收敛比较快,下面是这个问题的迭代路径,外迭代了 7 次就基本到达了最优解。
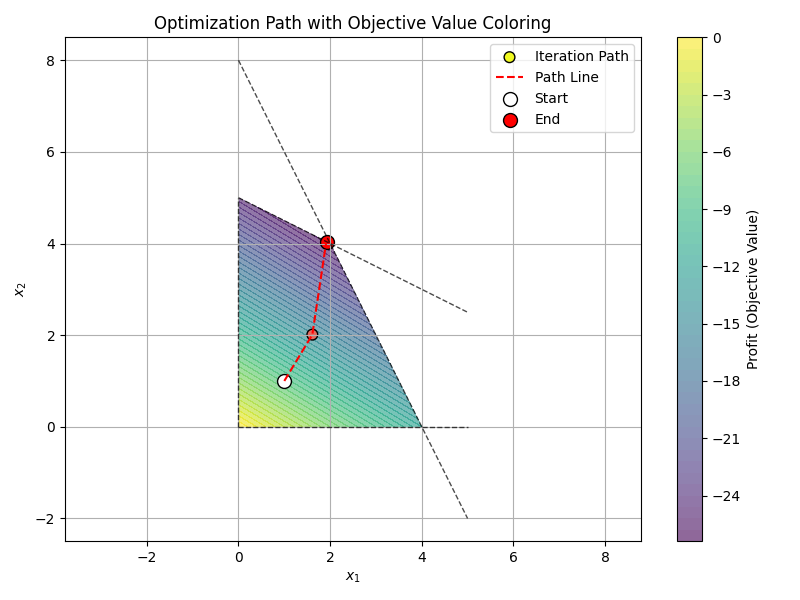
到现在,研究出了很多凸的问题,也研究出了很多算法。上面只是一些大概的介绍。读者可以继续学习。